Homomorphism in RSA
서론

해킹에 관심을 가지게 된 사람이라면 누구든지 그 실력을 기르기 위해 워게임(Wargame) 사이트에서 문제들을 풀거나 CTF(Capture The Flag) 대회에 출전해 본 적이 있을 것이다. 웹(Web), 리버싱(Reversing), 포너블(Pwnable) 등 여러 분야의 문제들을 만나볼 수 있는데, 특별한 경우를 제외하고 항상 등장하는 분야가 있다. 바로 암호학(Cryptography) 분야이다.
자주 등장하는 만큼 패기 있게 문제를 풀어보려 하지만 암호학 분야의 문제를 처음 접해보는 사람이라면 누구든지 괴상하게 뒤죽박죽 섞여 있거나 숫자로만 되어 있는 암호문을 받아보며 이것을 풀어서 정답을 제출하라는 말에 어떻게 해야 할지 시작부터 막막했던 경험이 있을 것이다.
이번 글에서는 암호학이라는 분야에 대해 막연히 어렵고 복잡하다고 생각하는 사람들을 위해 암호학 분야의 워게임 문제에서 가장 흔하게 나오고 실제 필드에서도 많이 쓰이는 공개키 암호화 기법의 기본 중의 기본, RSA 와 관련된 문제를 풀어보며 암호학이라는 게 그렇게 어렵고 막막하기만 한 것은 아니라는 점을 배워갈 수 있다면 좋겠다.
본론
그래서 RSA 가 뭔가요?

RSA 는 1978년에 최초로 이 암호시스템을 연구하여 체계화시킨 Ron Rivest, Adi Shamir, Leonard Adleman 의 이름 앞 글자를 따 만들어진 암호화뿐만 아니라 전자서명까지 가능한 최초의 알고리즘이다.
이 RSA 의 강력함은 다음 두 가지에서 나온다.
- 암/복호화, 서명/검증에 필요한 수학적인 계산 과정이 굉장히 간단하고 빠르다는 것.
- 큰 숫자의 소인수분해의 어려움을 이용한 강력한 안전성을 제공하고 있다는 것.
위 두 가지의 강점으로 인해 현재까지도 RSA 는 널리 쓰이고 있다.
다음으로는 왜 RSA 의 강점을 위 두 가지로 꼽았는지 키 생성부터 암/복호화, 서명/검증 과정을 살펴보며 알아보도록 하겠다.
RSA 키 생성
- 서로 다른 소수 p, q 를 랜덤하게 선택한다.
-
n = p * q 를 계산한다.
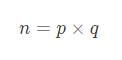
- n 에 대하여 오일러 피 함수(Euler’s phi (totient) function) 또는 카마이클 함수(Carmichael function) 중 하나를 선택하여 계산한다.
- 오일러 피 함수 (https://ko.wikipedia.org/wiki/오일러_피_함수)
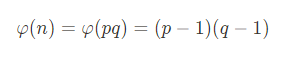
- 카마이클 함수 (https://en.wikipedia.org/wiki/Carmichael_function)
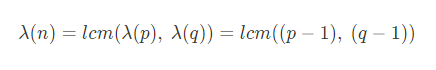
- 오일러 피 함수 (https://ko.wikipedia.org/wiki/오일러_피_함수)
-
3번에서 선택한 수와 서로소인 정수 e 를 고른다.
(두 정수 a, b 의 최대공약수(gcd)가 1 이면 둘은 서로소이다.)
(두 수가 서로소가 아니면 모듈러 역원을 구할 수 없다 → 개인키를 구할 수 없다.)
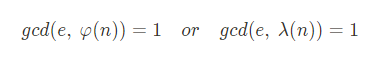
(일반적으로 계산의 효율성을 위해 페르마 수(Fermat Number)가 선택된다.)
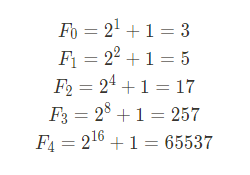
-
정수 e 에 대한 모듈러 역원인 d 를 계산한다.
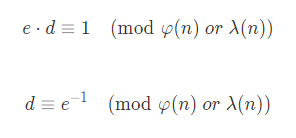
- 위에서 계산한 값들 중 n, e 를 공개키로써 배포하고, d 를 개인키로써 절대 노출되지 않게 한다.
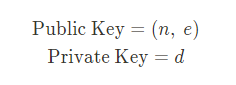
이제 해당 공개키를 이용하여 누구든지 메시지를 암호화해서 보내면 개인키를 가지고 있는 소유자만 해당 메시지를 복호화할 수 있다. 그렇다면 암/복호화는 어떻게 수행될까? 한번 살펴보자.
RSA 암호화
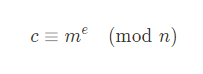
RSA 복호화
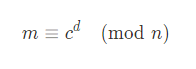
위와 같이 정말 간단하게 암/복호화가 수행되며 이에 대한 증명은 RSA 위키에 상세하게 나와있다.
(페르마 소정리, 오일러 정리를 이용하여 증명함)
이번에는 서명/검증이 어떻게 수행되는지 살펴보자.
RSA 서명
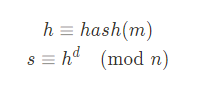
RSA 검증
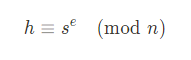
암/복호화 과정과 순서만 바뀌었을 뿐 거의 동일하게 서명/검증이 수행되며 서명 시 개인키 d 를 이용해 서명이 되기 때문에 누구에게나 공개되는 e 를 이용해 메시지 m 을 복원할 수 없도록 해시 함수를 이용하여 메시지 m 의 해시값인 h 에 서명을 진행하도록 한다.
메시지에 대한 서명이 완료되었다면 암호화된 메시지와 서명을 함께 전송하고 이후 검증 단계에서는 복호화된 메시지의 해시값과 s^e (mod n) 을 계산하여 나온 해시값 h 를 비교하여 일치하는지 확인하면 된다.
이제 RSA 시스템에 대한 기본적인 개념을 배웠으니 흥미로운 속성 하나를 추가로 알려주려고 한다.
준동형 사상(Homomorphism)
준동형 사상이란 대수학에서 구조상 닮은 두 대수 구조의 모든 연산 및 관계를 보존하는 경우를 말한다. 쉽게 말하자면, 어떠한 함수 f(x) 가 있다고 할 때 f(a * b) 가 f(a) * f(b) 와 같다는 것이다 (나눗셈도 마찬가지). 이는 신기하게도 RSA 에도 그대로 적용이 되는데 평문 m 이 a * b 라고 할 때 c ≡ m^e (mod n) 과 c ≡ (a * b)^e ≡ a^e * b^e (mod n) 이 서로 일치한다. 이는 서명에서도 마찬가지이며 예시를 통해 확인해보자.
예시
-
임의의 소수 p, q 선택
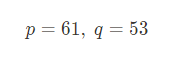
-
n = p * q 계산
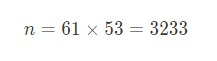
-
오일러 피함수 계산
.png)
-
오일러 피함수와 서로소인 정수 e 선택
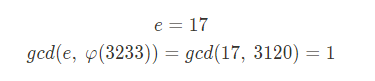
-
개인키 d 계산

-
평문 m = a * b 라고 할 때 암호화 과정 비교
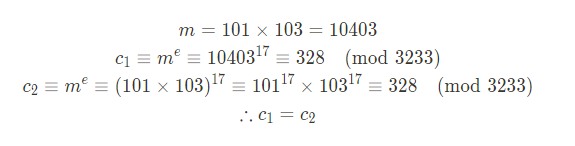
-
서명 과정 비교 (계산 편의를 위해 해시 함수는 미적용)
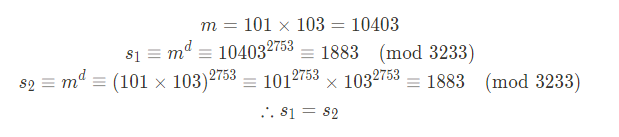
CTF 의 RSA 문제에서 위 속성을 이용한 문제가 꽤나 자주 출제되며 한번 실제로 출제된 문제를 풀어보며 어떤 식으로 응용되는지 살펴보자.
문제 풀이
- LINECTF2022
| 문제명 | X Factor |
|---|---|
| 난이도 | Easy |
| 설명 | Decrypt it! |
| 제공파일 | x_factor.md |
먼저, 제공된 파일을 열어서 확인해보자.
» Part 1
I have generated a RSA-1024 key pair:
* public key exponent: 0x10001
* public key modulus: 0xa9e7da28ebecf1f88efe012b8502122d70b167bdcfa11fd24429c23f27f55ee2cc3dcd7f337d0e630985152e114830423bfaf83f4f15d2d05826bf511c343c1b13bef744ff2232fb91416484be4e130a007a9b432225c5ead5a1faf02fa1b1b53d1adc6e62236c798f76695bb59f737d2701fe42f1fbf57385c29de12e79c5b3
첫번째로 RSA 공개키 쌍(Public Exponent: e, Public Modulus: n)을 16진수 형태로 제공해주고 있다.
» Part 2
Here are some known plain -> signature pairs I generated using my private key:
* 0x945d86b04b2e7c7 -> 0x17bb21949d5a0f590c6126e26dc830b51d52b8d0eb4f2b69494a9f9a637edb1061bec153f0c1d9dd55b1ad0fd4d58c46e2df51d293cdaaf1f74d5eb2f230568304eebb327e30879163790f3f860ca2da53ee0c60c5e1b2c3964dbcf194c27697a830a88d53b6e0ae29c616e4f9826ec91f7d390fb42409593e1815dbe48f7ed4
* 0x5de2 -> 0x3ea73715787028b52796061fb887a7d36fb1ba1f9734e9fd6cb6188e087da5bfc26c4bfe1b4f0cbfa0d693d4ac0494efa58888e8415964c124f7ef293a8ee2bc403cad6e9a201cdd442c102b30009a3b63fa61cdd7b31ce9da03507901b49a654e4bb2b03979aea0fab3731d4e564c3c30c75aa1d079594723b60248d9bdde50
* 0xa16b201cdd42ad70da249 -> 0x9444e3fc71056d25489e5ce78c6c986c029f12b61f4f4b5cbd4a0ce6b999919d12c8872b8f2a8a7e91bd0f263a4ead8f2aa4f7e9fdb9096c2ea11f693f6aa73d6b9d5e351617d6f95849f9c73edabd6a6fde6cc2e4559e67b0e4a2ea8d6897b32675be6fc72a6172fd42a8a8e96adfc2b899015b73ff80d09c35909be0a6e13a
* 0x6d993121ed46b -> 0x2b7a1c4a1a9e9f9179ab7b05dd9e0089695f895864b52c73bfbc37af3008e5c187518b56b9e819cc2f9dfdffdfb86b7cc44222b66d3ea49db72c72eb50377c8e6eb6f6cbf62efab760e4a697cbfdcdc47d1adc183cc790d2e86490da0705717e5908ad1af85c58c9429e15ea7c83ccf7d86048571d50bd721e5b3a0912bed7c
* 0x726fa7a7 -> 0xa7d5548d5e4339176a54ae1b3832d328e7c512be5252dabd05afa28cd92c7932b7d1c582dc26a0ce4f06b1e96814ee362ed475ddaf30dd37af0022441b36f08ec8c7c4135d6174167a43fa34f587abf806a4820e4f74708624518044f272e3e1215404e65b0219d42a706e5c295b9bf0ee8b7b7f9b6a75d76be64cf7c27dfaeb
* 0x31e828d97a0874cff -> 0x67832c41a913bcc79631780088784e46402a0a0820826e648d84f9cc14ac99f7d8c10cf48a6774388daabcc0546d4e1e8e345ee7fc60b249d95d953ad4d923ca3ac96492ba71c9085d40753cab256948d61aeee96e0fe6c9a0134b807734a32f26430b325df7b6c9f8ba445e7152c2bf86b4dfd4293a53a8d6f003bf8cf5dffd
* 0x904a515 -> 0x927a6ecd74bb7c7829741d290bc4a1fd844fa384ae3503b487ed51dbf9f79308bb11238f2ac389f8290e5bcebb0a4b9e09eda084f27add7b1995eeda57eb043deee72bfef97c3f90171b7b91785c2629ac9c31cbdcb25d081b8a1abc4d98c4a1fd9f074b583b5298b2b6cc38ca0832c2174c96f2c629afe74949d97918cbee4a
두번째로 (평문 - 서명) 쌍 7 개를 16진수 형태로 제공해주고 있다.
» Part 3
**What is the signature of 0x686178656c696f6e?**
Take the least significant 16 bytes of the signature, encode them in lowercase hexadecimal and format it as `LINECTF{sig_lowest_16_bytes_hex}` to obtain the flag.
E.g. the last signature from the list above would become `LINECTF{174c96f2c629afe74949d97918cbee4a}`.
세번째로 평문 0x686178656c696f6e 의 서명이 무엇인지 맞춰보라며 서명의 16진수 형태의 마지막 16 바이트를 FLAG 형식에 맞춰 제출하면 된다고 한다.
현재 우리가 알고 있는 정보는 공개키(e, n)와 (평문 - 서명) 쌍 7개, 그리고 FLAG 인 서명을 구하기 위해 필요한 평문 0x686178656c696f6e 뿐이다. 의미를 알 수 없는 16진수 형태의 숫자로만 가득한 텍스트로부터 어떻게 개인키 d 도 없이 서명을 구할 수 있을까?
바로 위에서 배운 준동형 사상(Homomorphism)을 이용하여 풀면 된다.
먼저 평문 0x686178656c696f6e 을 소인수분해 해보면 다음과 같다 (SageMath 의 factor 함수):
# Implemented in SageMath
target = 0x686178656c696f6e # 7521425229691318126
factor(target) # 2 * 197 * 947 * 2098711 * 9605087
위와 같이 5 개의 소인수의 곱으로 평문을 표현할 수 있다는 것을 알 수 있다. (m = a * b * c * d * e)
이번에는 주어졌던 (평문 - 서명) 쌍에서 평문들만 소인수분해 해보면 다음과 같다:
pt1 = 0x945d86b04b2e7c7
pt2 = 0x5de2
pt3 = 0xa16b201cdd42ad70da249
pt4 = 0x6d993121ed46b
pt5 = 0x726fa7a7
pt6 = 0x31e828d97a0874cff
pt7 = 0x904a515
pts = [pt1, pt2, pt3, pt4, pt5, pt6, pt7]
for i in range(7):
print(f"pt{i+1}: ", pts[i])
print(f"factor(pt{i+1}): ", factor(pts[i]))
print()
'''
[+] Output:
pt1: 668178073886320583
factor(pt1): 811 * 947^3 * 970111
pt2: 24034
factor(pt2): 2 * 61 * 197
pt3: 12196433909207788967273033
factor(pt3): 970111 * 2098711^2 * 2854343
pt4: 1928075547694187
factor(pt4): 947 * 970111 * 2098711
pt5: 1919920039
factor(pt5): 61 * 197^2 * 811
pt6: 57538707471611677951
factor(pt6): 2098711 * 2854343 * 9605087
pt7: 151299349
factor(pt7): 197 * 811 * 947
'''
신기하게도 몇몇 소인수들이 평문 0x686178656c696f6e 의 소인수들과 겹친다는 것을 확인할 수 있다. 소인수가 겹치는게 뭐 어떻길래 그런걸까? 우리는 7 개의 (평문 - 서명) 쌍을 알고 있기 때문에 해당 평문을 잘 조합해서 평문 0x686178656c696f6e 과 일치하게 만든다면 RSA 에서의 준동형 사상으로 인해 평문 0x686178656c696f6e 에 개인키 d 를 이용하여 계산한 서명과 동일한 서명을 개인키 d 없이도 구할 수 있게 된다.
이게 무슨 소리?
위에서 평문 0x686178656c696f6e 이 5 개의 소인수의 곱 형태로 표현이 가능하다는 것을 알았다.
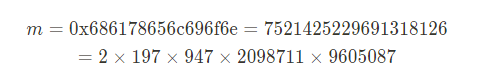
우리는 개인키 d 를 모르기 때문에 m 에 대한 서명을 구할 수 없지만, 7 개의 (평문 - 서명) 쌍을 알고 있고 각 평문의 소인수가 평문 0x686178656c696f6e 의 소인수와 겹치기 때문에 곱하기와 나누기를 적절히 이용하여 평문 0x686178656c696f6e 과 일치하는 수를 구할 수 있다면 해당 수를 구했을 때의 식과 동일하게 7 개의 서명에 적용하여 계산하면 평문 0x686178656c696f6e 에 개인키 d 를 이용하여 계산한 서명과 동일한 서명을 개인키 d 없이도 구할 수 있게 된다는 말이다.

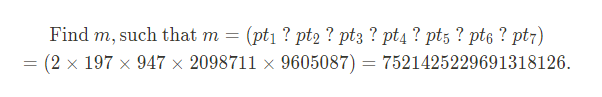
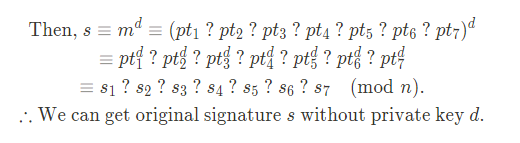
(현재로써는 곱하기, 나누기 중 어떤 연산자가 들어가야 하는지 모르기 때문에 물음표(’?’)로 두었다.)
평문 0x686178656c696f6e (target)과 일치하는 수를 구하기 위해서는 약간의 머리를 써서 7 개의 평문을 곱하고 나누면 된다. 나의 경우에는 작은 소인수를 가진 평문부터 순서대로 나열해보았다.
pt2 : 2 * 61 * 197
pt5 : 61 * 197^2 * 811
pt7 : 197 * 811 * 947
pt1 : 811 * 947^3 * 970111
pt4 : 947 * 970111 * 2098711
pt3 : 970111 * 2098711^2 * 2854343
pt6 : 2098711 * 2854343 * 9605087
-----------------------------------------------------------------------------
target: 2 * 197 * 947 * 2098711 * 9605087
이제 곱하기, 나누기를 이용하여 target 과 일치하는 수를 만들면 된다.
pt2: 2 * 61 * 197
(/) pt5: 61 * 197^2 * 811
-----------------------------------------------------------------------------------------
2 * 197^(-1) * 811^(-1)
(*) pt7: 197 * 811 * 947
-----------------------------------------------------------------------------------------
2 * 947
(*) pt7: 197 * 811 * 947
-----------------------------------------------------------------------------------------
2 * 197 * 811 * 947^2
(/) pt1: 811 * 947^3 * 970111
-----------------------------------------------------------------------------------------
2 * 197 * 947^(-1) * 970111^(-1)
(*) pt4: 947 * 970111 * 2098711
-----------------------------------------------------------------------------------------
2 * 197 * 2098711
(*) pt4: 947 * 970111 * 2098711
-----------------------------------------------------------------------------------------
2 * 197 * 947 * 970111 * 2098711^2
(/) pt3: 970111 * 2098711^2 * 2854343
-----------------------------------------------------------------------------------------
2 * 197 * 947 * 2854343^(-1)
(*) pt6: 2098711 * 2854343 * 9605087
-----------------------------------------------------------------------------------------
answer: 2 * 197 * 947 * 2098711 * 9605087
Therefore, answer = pt2 / pt5 * pt7^2 / pt1 * pt4^2 / pt3 * pt6.
7 개의 평문을 이용하여 평문 0x686178656c696f6e (target)과 일치하는 수(answer)를 구했기 때문에 이제 7 개의 서명을 이용하여 동일한 식으로 target 의 서명을 구할 수 있다.
아래는 target 의 서명과 FLAG 를 구하기 위해 사용한 코드이다.
# Implemented in SageMath
target = 0x686178656c696f6e
print("target: ", target) # 7521425229691318126
print("factor(target): ", factor(target)) # 2 * 197 * 947 * 2098711 * 9605087
print()
answer = pt2 / pt5 * pt7^2 / pt1 * pt4^2 / pt3 * pt6
print("answer: ", answer) # 7521425229691318126
print("factor(answer): ", factor(answer)) # 2 * 197 * 947 * 2098711 * 9605087
print()
assert target == answer
# Using the same formula as answer including modular n.
# This is possible because of the homomorphism in unpadded RSA.
newsig = (sig2 / sig5 * sig7^2 / sig1 * sig4^2 / sig3 * sig6) % n
print("newsig (int): ", newsig)
# 111219533890621461179460792242241632450808153632799554790302537773885731996725665970159819970061237994467913213678895572474822930918390150774003109045699291202079975387595071497569834504251162974827309324614046581068300485342202365281472704413710935864495616184160512233863134373547246784976501532318112012352
newsig = hex(newsig)[2:]
print("newsig (hex): ", newsig)
# 9e61c276f698ec48aab7dabfd663f3b2ee75d31c68bf16f6810a3bb9bb1c377e47b2ae8cd7055c7c5848bbedc94798d2965c38b317e42191df0e3f25ca2ee58c5f3e125745479b337516a13e420da29ba48a92ca2ee9720487cda6cdf070e83a4a251c52e331174a0ef642a97a251462a049347a7db8226d496eb55c15b1d840
print()
'''
Take the least significant 16 bytes of the signature, encode them in lowercase hexadecimal and format it as `LINECTF{sig_lowest_16_bytes_hex}` to obtain the flag.
E.g. the last signature from the list above would become `LINECTF{174c96f2c629afe74949d97918cbee4a}`.
'''
flag = 'LINECTF{' + str(newsig[-32:]) + '}'
print("flag: ", flag)
# flag: LINECTF{a049347a7db8226d496eb55c15b1d840}
결론

지금까지 RSA 란 무엇인지, 키 생성, 암/복호화, 서명/검증은 어떻게 이루어지는지 알아보았고, 또 대수학에서의 준동형 사상(Homomorphism) 개념을 CTF 에서 자주 출제되는 유형의 RSA 문제에 적용하여 풀어보았다. 이외에도 수많은 방식의 RSA 공격 기법들이 존재하지만 대부분 위 문제 풀이에서 본 것과 같이 수학적인 개념을 가지고 사칙연산만 할 줄 안다면 금방 이해하고 그것을 문제에 적용할 수 있을 것이다.
암호를 푼다는 것은 얽히고설킨 실타래를 푸는 것과도 같다고 생각한다. 처음 문제를 접했을 때는 도무지 어떻게 이것을 풀어야 한다는 건지 감을 잡을 수조차 없지만 천천히 둘러보다 보면 문제를 해결할 수 있는 실마리를 잡을 수 있을 것이다. 이 글이 암호학 문제를 푸는 이들에게 좋은 시작점이 되기를 기원하며 글을 마무리하도록 하겠다.

